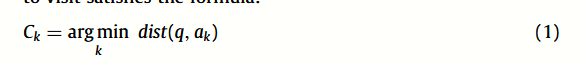Two-stage routing with optimized guided search and greedy algorithm on proximity graph

论文简介

Two-stage routing with optimized guided search and greedy algorithm on proximity graph 是王梦召在2021年发表于 Knowledge-Based Systems 上的期刊文章。

Abstract

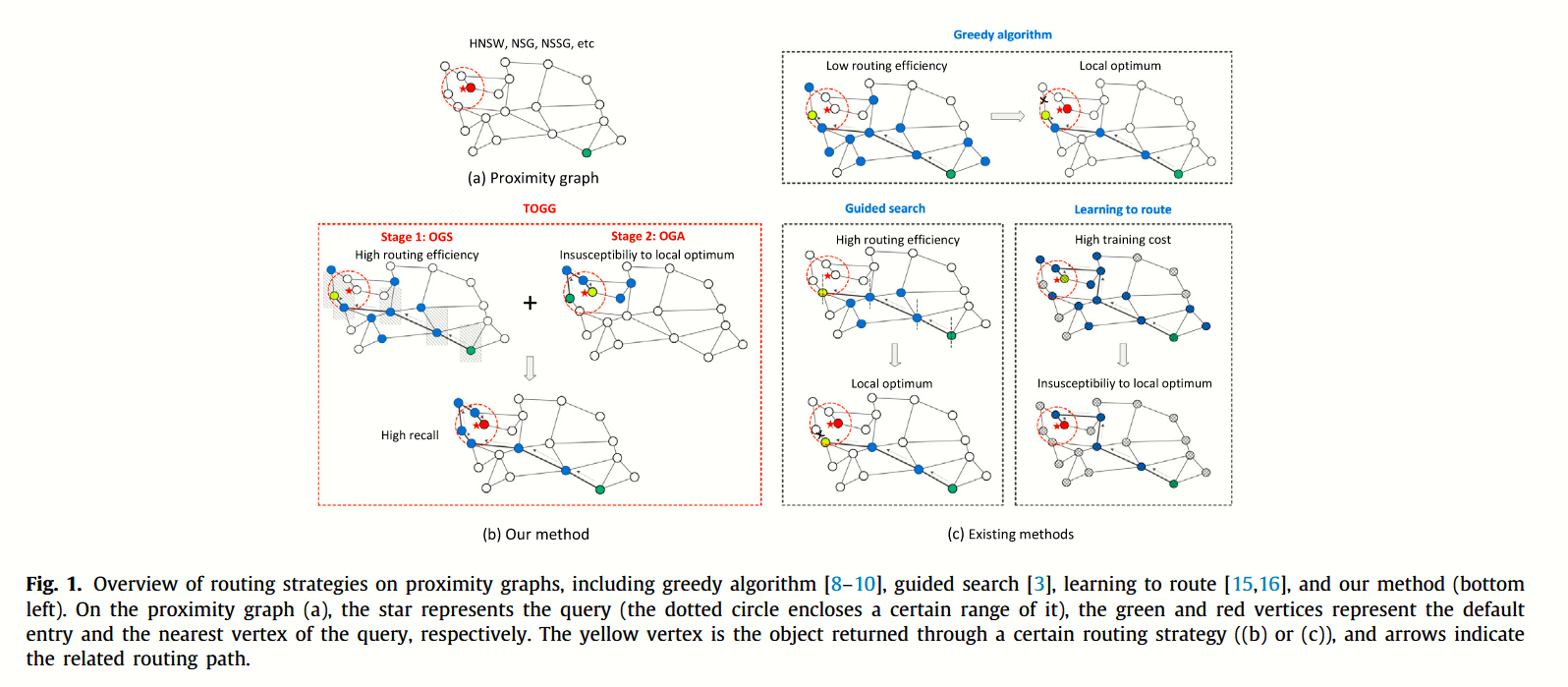
随着人们对大规模检索任务的兴趣激增，邻近图现在已成为领先的范例。现有的邻近图大多采用简单的贪心算法作为近似最近邻搜索（ANNS）的路由策略，但这会导致两个问题：路由效率低和局部最优；这是因为他们忽略了不同路由阶段的特殊要求。一般来说，路由可以分为两个阶段：远离查询的阶段（S1）和靠近查询的阶段（S2）。 S1旨在快速路由到查询附近，效率占优。而S2注重的是准确地找到结果，所以准确度是最重要的。我们为每个阶段精心设计定制的路由算法，然后将它们组合在一起形成优化引导搜索和贪心算法（TOGG）的两阶段路由。对于S1，我们提出优化的引导搜索，通过查询方向的引导快速定位查询的邻域。而对于S2，我们提出了优化的贪心算法，通过敏捷地检测显式和隐式收敛路径来全面访问查询附近的顶点。最后，通过理论和实验分析，我们证明所提出的方法可以实现比最先进的工作更好的效率和效果。

内容

1、Introduction

这部分讲述了一下贪心算法导致的两个问题：

1、路由效率低下，每步都要加载所有的邻居并比较。

2、局部最优解，贪心算法不可避免地有陷入局部最优解的可能性。

针对1，有工作提出了只访问同一方向的邻居的思想，但是容易丢失重要路径、以及在最终优化阶段会丢失掉更多的重要结果。

针对2，论文指出了学习索引可以解决局部最优的问题，也就是 Learning to Route in Similarity Graphs 这篇工作。

论文将导航流程归类为两个阶段，far from 和 closer to 。阶段1主要的目标是尽可能快地定位到近邻区域，阶段2的目标是精细化地查找邻居保障结果准确性。

在这个部分，论文提出了他们这样划分的创新性，并简述了研究动机。

2、Related work

这部分中，论文从近邻图和路由选择策略上分别简述了相关工作，以及和本篇工作的相关性。

近邻图

论文简述了 HNSW 、 NSG 、 NSSG 这三个拥有相似贪心导航算法的近邻图。并说明了论文是基于这三个图来实现的。

导航策略

论文针对共用的贪心导航算法中共同存在的问题，分别简述了一些工作。也就是 Introduction 中问题的详细描述：

1、导航效率低下：Hierarchical clusteringbased graphs for large scale approximate nearest neighbor search

2、局部最优解：Learning to route in similarity graphs

3、Two-stage routing strategy with optimized guided search and greedy algorithm

3.1 Motivation example

这部分是论文的重点部分。首先，论文通过几个例子分析了以往邻近图中路由策略存在的问题。接下着提出了一个新的路由框架，称为first-coarse-last-refinement，它包括两部分。

对于粗略导航阶段，论文提出优化引导搜索（OGS），它可以快速定位查询附近并确保路线沿着正确的路径。对于最后的细化阶段，论文采用优化贪心算法（OGA）在查询附近的小区域内进行精确搜索。最后，基于这个框架，论文展示了TOGG路由过程——这是一种OGS和OGA的混合路由策略——以实现优势互补。

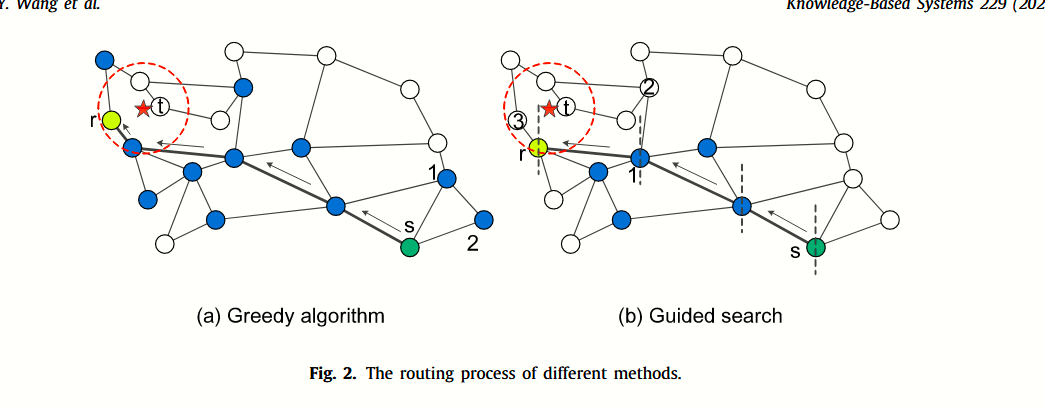
alt text

alt text

上图是问题分析的图示，下面是几个问题的例子：

1、Fig. 2(a) 图中表示了节点 1、2 是传统贪心算法需要计算的节点，但是节点与目标的方向是完全不相干的，因此可以排除。

2、Fig. 2(a) 图中，同样表示了局部最优的问题。点r并不是最优解，但是由于其是局部最优，因此还是终止了查询。

3、Fig. 2(b) 图中，表示了，当贪心选择到节点1时，节点2虽然不与目标方向一致，但是仍然是通往目标的唯一路径。但是根据方向排除路由，将导致2不被访问。这个示例主要针对 Hierarchical clusteringbased graphs for large scale approximate nearest neighbor search 一文中，面对终止的细化搜索时的不足。

4、Routing framework: First-coarse-last-refinement

论文在这部分简单介绍了算法的框架。

为了快速定位到邻居旁，论文以划分空间的方式划分每个顶点的邻居集。KD-Tree（KDT）[18,35]可以根据方向将邻居集划分为多个子树，k-means clustering（KMC）可以根据方向将邻居集划分为多个簇。因此，对于第一个粗略部分，文提出了基于改进的KDT和KMC的优化引导搜索（OGS）；它们针对不同的数据集和邻近图有各自的优势，可以快速准确地定位到查询的附近。

因此，论文分别实现了对应索引结构下的导航算法。

4.1.1 modified KDT

什么是 KD Tree :

CMU CMSC 420 课件：https://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/kdtrees.pdf

在欧氏空间中，给定一个包含 n 个点的有限数据集 S，第 j (j = 0, 1, …, d − 1) 维中每个数据点的最大值为 maxj，最小值为 minj, p为S中任意一点，其在第j维的值为pj，G表示在S上定义的图，p在G中的邻居集合为N(G,p)，预设比例值为1/b。设gj = (maxj − minj)/b，则±gj为第j维划分区间的边界。

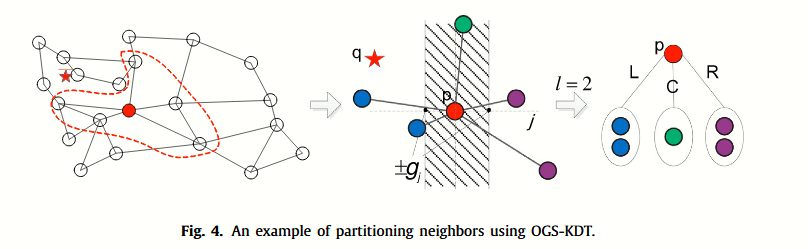
alt text

上图是论文的变形KDT的划分算法，下图是一个划分示例：

alt text

简单的说，这个KDT其实就是将某个节点p的全部邻居，用两个超平面划分开为三部分进行归类。gj是一个受b影响的可变条件，它控制着超平面的距离。事实上，这个索引结构只根据单维进行划分，因此可能会有较大误差。但是胜在简单和快速。

在搜索时，查询q如果导航到了节点p，将把q也进行一次同样的划分，然后根据q所在的部分，返回同样部分的节点，如下面的伪代码所示：

alt text

4.1.2 Optimized guided search based on KMC

简单来说，把所有的邻居做 k-means 聚类，然后用聚类中心点和q的距离做筛选。

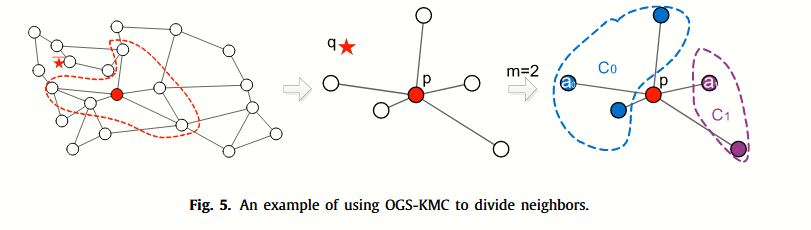
alt text

给定空间 Ed 中包含 n 个点的有限数据集 S，p 是 S 中的点，G 是 S 上定义的图，p 在 G 中的邻居集是 N(G, p)，其中 N(G, p)根据k-means聚类分为m个簇，第k个簇的中心为ck，属于第k个簇的邻居顶点集合为Ck。近似聚类中心是ak，它是ck 的最近邻，ak​​ ∈ Ck，其中k = 0, 1,…。 。 。 ，m − 1。在路由阶段，q为查询，遍历到顶点p时，需要访问的Ck满足公式：

alt text

其中 dist(q, ak) 是 q 和 ak 之间的距离。

路由的示例如下图：

alt text

在索引阶段，节点p的邻居被划分为两个聚类。查询阶段，比较两个聚类中心点距离q的距离，只使用距离最近的聚类作为候选节点。下面是伪代码：

alt text

4.2 Optimized greedy algorithm

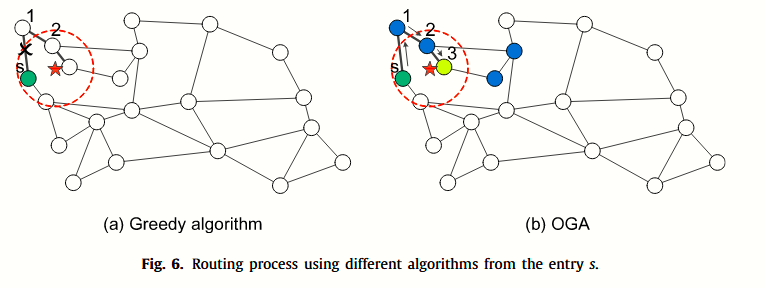
在靠近查询的路由阶段，根据查询的方向继续访问邻居是不合理的。否则，由于示例3所示的问题，引导策略会严重损害返回结果的准确性。因此，论文提出优化的贪婪算法（OGA）来更好地实现最后的细化部分。

1.Convergence Path 收敛路径

给定空间 Ed 中 n 个点的有限数据集 S，p、q 是 S 中的任意两点，G(V , E) 是在 S 上定义的图，V 和 E 分别是顶点集和边集。 v1、v2、. 。 。 , vi (v1 = p, vi = q) 表示 G 中从 p 到 q 的路径，即 ∀j = 1, 2,…。 。 。 , i − 1, 边 vjvj+1 ∈ E。这条路径是一条收敛路径 iff ∀j = 1, 2, 。 。 。 , i−1, dist(vj, q) > dist(vj+1, q)，其中 dist(, ) 是距离。

定义如上。简言之，就是一条单调路径，和 NSG 这篇论文中提到的单调路径一致。在路径上，每个节点都不断地更接近查询点q。

alt text

OGA不仅访问候选集中每个顶点的邻居（检测显式收敛路径），还访问邻居的邻居（检测隐式收敛路径），从而判断是否需要从某个邻居继续扩展。如果存在从当前邻居到查询附近的隐式收敛路径，OGA 继续沿着它扩展（算法 5 中的第 10-17 行）。与贪心算法相比，OGA 放松了扩展约束，从而减轻了局部最优问题。

alt text

简而言之，OGA 是一个通过添加多一跳来避免陷入局部最优的小改进。

4.3 TOGG routing process

路由过程。

alt text

如上述伪代码，路由过程是简单的两个阶段，都分别执行到不能再优化为止。

接着论文又简述了HNSW的优化，说明了两者的差异和兼容性。

5、Algorithm complexity and parameters analysis

这部分就不看了，没什么特别重要，主要分析了两类索引构建和查询的时间复杂度，以及新添加的 OGA 的时间复杂度。

6、Experiments

论文实验用的数据集：SIFT1M,2 GIST1M,3 GloVe,4 and MNIST,

论文的 baseline 选用了四个工作：

  1. Fast approximate similarity search based on degree-reduced neighborhood graphs （SIGKDD’2011）

  2. Fanng: Fast approximate nearest neighbour graphs （CVPR’2016）

  3. Hierarchical clusteringbased graphs for large scale approximate nearest neighbor search （PR’2019）

  4. High dimensional similarity search with satellite system graph: Efficiency, scalability, and unindexed query compatibility （TPAMI’2021）

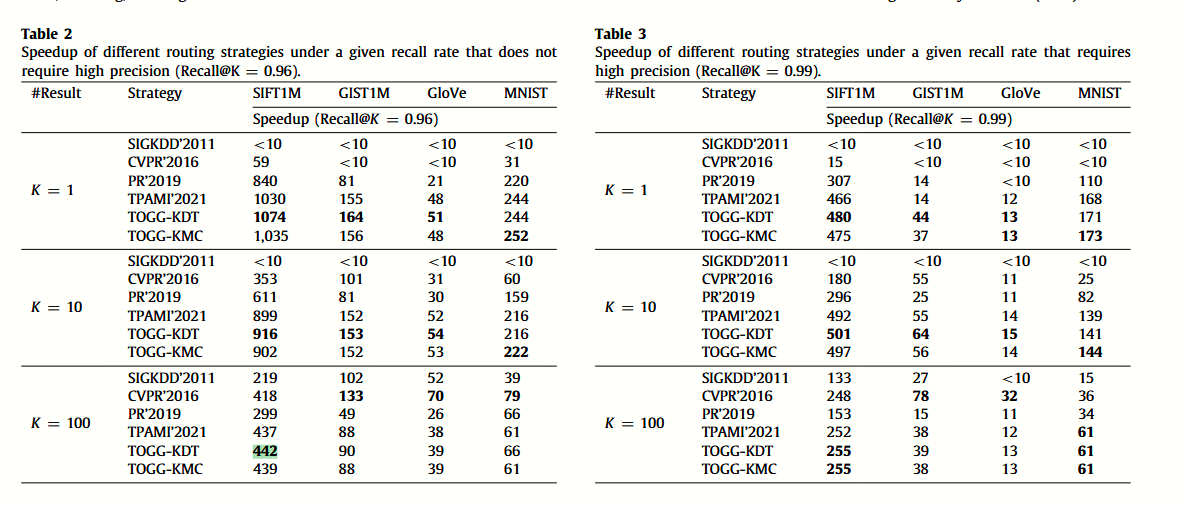
论文有两个实验指标，加速比和召回率指标为：

alt text

alt text

在保证召回率一致的前提下，论文比较了多个路由选择策略的效果：

alt text

总地说，论文的策略略好于 SOTA TPAMI’2021 。